Kapitän Heiner

Umfassende Übungsaufgabe zum Monopol

apitän Heiner lebt auf der Insel Eiland und bietet den Insulanern täglich eine Überfahrt zum Festland an. Aus Erfahrung weiß er, dass ihm mit jeder Überfahrt unabhängig von der Zahl der Passagiere 14 Euro Kosten entstehen. Für jeden Passagier kalkuliert er 2 Euro an zusätzlich anfallenden Kosten (erhöhter Kraftstoffverbrauch, Fahrkarte, Fahrkartenverkauf, Reinigungskosten etc.).

Die Nachfrage nach Kapitän Heiners Überfahrten kann durch die Preis-Absatz-Funktion $p = 10 - 0,5x$ angegeben werden (mit $p$ als Preis für eine Fahrkarte und $x$ als Zahl der Passagiere). Heiners Schiff ist für 25 Passagiere zugelassen.

Einblenden a) Geben Sie die Kostenfunktion an.

Die Kostenfunktion lautet $C = 14 + 2x$.

Einblenden b) Geben Sie die Grenzumsatzfunktion an.

Die Grenzumsätze werden angezeigt durch die Preis-Absatz-Funktion mit doppelter Steigung, wenn die Preis-Absatz-Funktion eine Gerade ist; also: $\cfrac{\text{d}U}{\text{d}x} = 10 - x$.

Einblenden c) Welche Passagierzahl maximiert seinen Umsatz?

Der Umsatz ist maximal, wenn der Grenzumsatz gleich null ist (notwendige Bedingung). Das ist offensichtlich bei 10 Passagieren der Fall (d. b)). Dass es sich um ein Maximum handelt, ist offensichtlich. Deshalb kann eine Überprüfung der hinreichenden Bedingung unterbleiben.

Einblenden d) Fertigen Sie eine maßstabsgetreue Zeichnung zur Ableitung des Cournotschen Punktes an.

Abbildung 1

Über die Regel "Grenzumsatz= Grenzkosten" findet man den Cournotschen Punkt C. Würde sich Kapitän Heiner wie ein Anbieter bei vollkommener Konkurrenz verhalten, dann würde er in K zu einem geringeren Preis eine größere Menge anbieten. Die fallenden Durchschnittskosten lassen ein Konkurrenzangebot aber nicht zu, denn die durchschnittlichen (totalen) Kosten DTK liegen immer über den Grenzkosten (und somit über dem Preis).

Einblenden e) Geben Sie den Monopolpreis an.

Mit der Regel „Grenzumsatz = Grenzkosten“ folgt:
$10 - x = 2$
$ x = 8 $
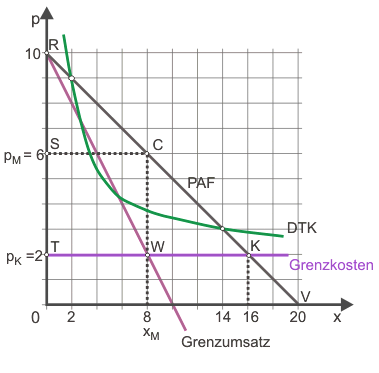
In der Grafik ist diese Menge als x_M eingezeichnet. Durch Einsetzen in die Preis-Absatz-Funktion wird der gewinnmaximierende Preis als 6 ermittelt.

Einblenden f) Überprüfen Sie, ob die hinreichende Bedingung für Gewinnmaximierung erfüllt ist.

Die hinreichende Bedingung lautet $U'' \lt C''$. Dies ist der Fall, denn in Abbildung 1 erkennt man einen negativen Wert für die zweite Ableitung der Umsatzfunktion (ihre erste Ableitung, die Grenzumsatzfunktion, hat eine negative Steigung), während die Grenzkosten konstant sind, also die zweite Ableitung der Kostenfunktion null ist.

Einblenden g) Geben Sie den maximalen Gewinn an.

$G^* = U - C = 6 \cdot 8 - (14 + 2 \cdot 8) = 18 $

Einblenden h) Die Eiländer beschweren sich eines Tages beim Inselvorsteher, Heiner würde sie mit seinem monopolistischen Preis ausbeuten. Daraufhin bestimmt der Inselvorsteher einen Höchstpreis von 2 Euro pro Überfahrt. Was hätte dieser Preis für sich?

Ein Preis von 2 Euro hätte sich auch mit der Regel "Preis = Grenzkosten" eingestellt. Dies ist der Preis, den Heiner gefordert hätte, wenn er sich wie ein Anbieter bei vollkommener Konkurrenz verhalten hätte. Bei einem Preis von 2 Euro würde mit 16 Passagieren pro Fahrt die gesellschaftlich optimale Menge "produziert". Die Summe aus Konsumenten- und Produzentenrente wäre maximal und alle Konsumenten mit einer Zahlungsbereitschaft größer gleich den Grenzkosten würden befördert.

Einblenden i) Heiner argumentiert, mit 2 Euro käme er nicht auf seine Kosten. Bestimmen Sie den niedrigsten Preis, mit dem Heiner die Kosten decken könnte.

Dieser Preis hätte einen Gewinn in Höhe von null zur Folge, so dass er sich aus
$G = U - C = (10 - 0,5x)x - (14 - 2x) = 0$
bestimmen lässt. Diese quadratische Gleichung hat die Lösungen $x_1 = 2$ und $x_2 = 14$. Dazu berechnet man über die Preis-Absatz-Funktion Preise in Höhe von 9 bzw. 3 Euro je Fahrschein. Der geringste Preis, mit dem Heiner seine Kosten decken könnte, betrüge also 3 Euro. In der Abbildung stimmen die durchschnittlichen totalen Kosten mit dem Preis überein (der Stückgewinn ist dann gleich null, so dass auch der Gewinn null ist).
Würde der Inselvorsteher das Monopol also durch das Gebot regulieren, den Preis in Höhe der Grenzkosten zu setzen, würde Heiner seinen Bootsbetrieb einstellen. Formal erkennt man das Scheitern dieser Regulierung entweder an Heiners sinkenden Durchschnittskosten (natürliches Monopol) oder daran, dass die hinreichende Bedingung für Gewinnmaximierung bei vollkommener Konkurrenz nicht erfüllt ist (steigende Grenzkosten). Der Inselvorsteher sollte sich eine alternative Regulierung einfallen lassen (z.B. könnte er das Recht, den Bootsbetrieb zu betreiben, von Jahr zu Jahr versteigern, wobei jeweils der Bieter den Zuschlag erhält, der den geringsten Fahrpreis fordert).

Einblenden j) Bestimmen Sie die Konsumentenrente, wenn der Monopolpreis verlangt wird.

Die Konsumentenrente entspricht der Fläche unter der Nachfragefunktion oberhalb des Preises (Dreieck RSC in Abbildung 1). Die Konsumentenrente beträgt damit 16 Euro.

Einblenden k) Bestimmen Sie die Konsumentenrente für den Fall, dass Heiner wie ein Anbieter bei vollkommener Konkurrenz handeln würde. Erklären Sie die Differenz in den Renten.

Bei vollkommener Konkurrenz wäre der Preis gleich den Grenzkosten, also 2 Euro. Die Konsumentenrente entspricht also der Fläche des Dreiecks TKR und beträgt 64 Euro. Die Differenz zur Konsumentenrente bei Konkurrenz setzt sich aus zwei Komponenten zusammen. Erstens entsteht durch das Monopol ein Allokationsverlust in Höhe des Dreiecks WKC. Zweitens: Dem Monopolist gelingt es im Vergleich zur Lösung bei Konkurrenz, das Rechteck TWCS von der Konsumentenrente abzuschöpfen. Die Fläche dieses Rechtecks zeigt einen Gegenwert von 32 Euro. Um diesen Betrag liegt der Monopolgewinn über dem Konkurrenzgewinn (Der Konkurrenzgewinn wäre hier ein Verlust in Höhe der fixen Kosten von 14 Euro).

Einblenden l) Wie ändert sich der Monopolpreis, wenn Heiners Gewinn mit 25 Prozent besteuert wird?

Gar nicht. Nach wie vor erzielt Heiner mit 8 Passagieren den höchsten Gewinn.

Einblenden m) Bestimmen Sie den Monopolgrad.

Der Lerner'sche Monopolgrad $ LR = (p_M -p_K)/p_M = (6-2)/6 = 66,66 %$. Die direkte Preiselastizität der Nachfrage im Cournotschen Punkt ist demzufolge -1,5.
Am Rande eine etwas fortgeschrittene Überlegung zu einer Fehlerquelle bei der Berechnung des Monopolgrades aus Monopol- und Konkurrenzpreis: Wenn die Grenzkosten nicht wie in diesem Beispiel konstant sind, darf man nicht jenen Konkurrenzpreis in die Lerner'sche Monopolgradformel einsetzen, den man über die Regel "Preis gleich Grenzkosten" ermittelt hat. Wenn die Grenzkosten ansteigen, würde man mit dem so ermittelten Konkurrenzpreis einen zu niedrigen Monopolgrad berechnen, da bei Konkurrenz eine größere Menge und somit zu höheren Grenzkosten produziert wird. Für einen fairen Vergleich muss man also bestimmen, zu welchem Preis ein Konkurrenzanbieter die Monopolmenge anbieten würde. Man muss also die Grenzkosten für die Monopolmenge berechnen und für den Konkurrenzpreis in die Lerner'sche Monopolgradformel einsetzen. Man spart sich diese Überlegung, wenn man sofort den negativen umgekehrten Wert der direkten Preiselastizität der Nachfrage im Cournotschen Punkt als Monopolgrad ausweist.

Die Aufgabe samt Lösung als -Datei .